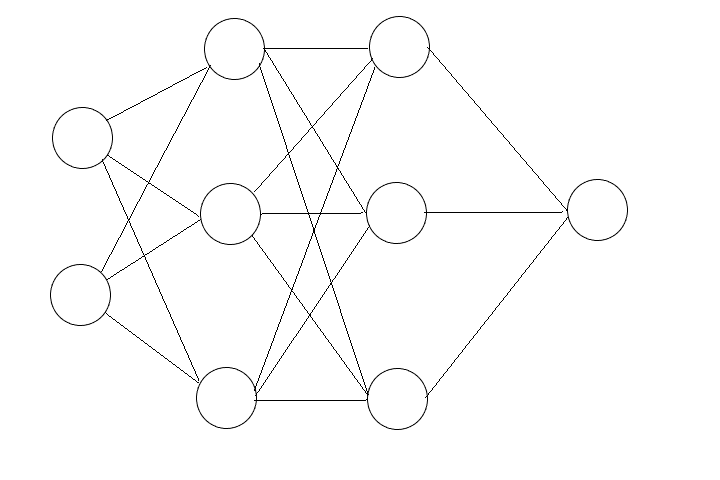
这是一个全连接神经网络的简图,由一个输入层,两个隐藏层和一个输出层构成
在这篇文章中,我将详细的讲讲它和其它类似的神经网络怎么工作,以及反向传播的完整推导过程
神经元
将一个神经元放大来看,大概是这样:
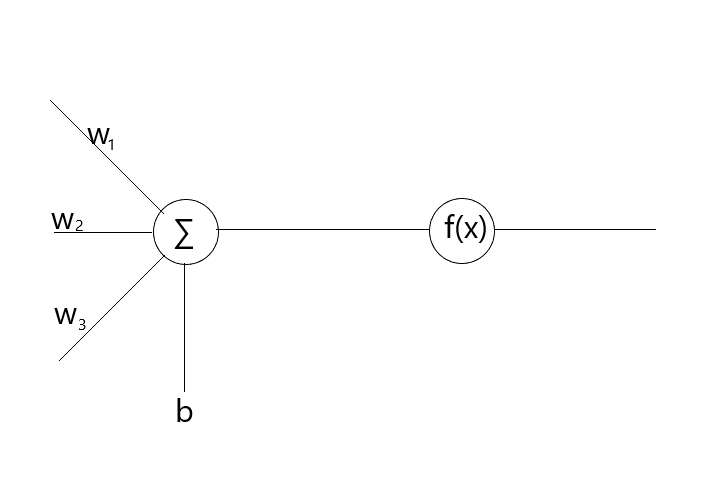
其中, $w_i$ 是权重, $b$ 是偏置, $f(x)$ 是激活函数
激活函数有很多种,常用的有 Sigmoid, ReLU 等,但它们的目的都是为了增强网络的拟合能力,进行非线性的拟合
激活函数必须是非线性的
令 $n$ 为输入数量, $x_i$ 为每个输入的值
在激活之前,它的输出为输入加权求和后的值。即 $q=\sum_{i=1}^nw_ix_i+b$
激活之后,它的输出为: $r=f(q)$
请务必记牢这两个式子,后面会频繁地使用它们
约定
网络层数(不包括输入层): $T$
网络输入数量: $n_0$
第 $k$ 层神经元数量: $n_k$
第 $k$ 层的激活函数: $f_k(x)$
连接第 $k$ 层第 $i$ 个神经元与上一层第 $j$ 个神经元的权重: $w_{kij}$
第 $k$ 层第 $i$ 个神经元的偏置: $b_{ki}$
网络的第 $i$ 个输入: $r_{0i}$
第 $k$ 层第 $i$ 个神经元激活前的输出: $q_{ki}$
第 $k$ 层第 $i$ 个神经元激活后的输出: $r_{ki}$
前向传播
之前,我们已经知道了每一个神经元的工作方法
那么这一步十分简单,用一样的方法即可
$$q_{ki}=\sum_{j=1}^{n_{k-1}}w_{kij}r_{{k-1}j}+b_{ki}$$
$$r_{ki}=f_k(q_{ki})$$
最后一层神经元激活后的输出,就是整个神经网络的输出
训练
到目前为止,我们还有一个很大的问题:参数从哪来?
类似于网络层数、神经元数量这些关于网络结构以及之后要说的训练过程的参数,我们称为超参数
这些参数通常由网络设计者来设定
而权重和偏置,手动设定显然不现实。所以,我们通过让网络自己学习这些参数,这就是训练
为了训练神经网络,首先要设计一个损失函数,用来评估模型的准确度
如 $L(x_1, x_2, … x_{n_T}, y_1, y_2, … y_{n_T})=\sum_{i=1}^{n_T}(x_i-y_i)^2$ 就是一种常用的损失函数
我们令期望输出的第 $i$ 个值为 $y_i$
我们令损失值 $l=L(r_{T1}, r_{T2}, … r_{Tn_T}, y_1, y_2, … y_{n_T})$
想要找到最合适的参数,就是找到 $l$ 的低谷
我们可以通过一些方法求出 $\dfrac{\partial l}{\partial w_{kij}}$ 和 $\dfrac{\partial l}{\partial b_{ki}}$
求出了微分,我们就能够知道如何调整参数才能让 $l$ 尽可能快地减小
这就是梯度下降法
我们使用优化器这一概念来描述调整的方法,我们令其为 $O(w, d, \eta)$
最简单的一种就是 $O(w, d, \eta)=w-\eta d$
其中的 $\eta$ 指学习率,这也是个超参数
通常情况下,太高的学习率会导致损失值不稳定,太低会导致学习过慢
一般,我们可以取 $\eta=0.01$
这样一来,只需不断使
$$w_{kij}\gets O\left(w_{kij}, \dfrac{\partial l}{\partial w_{kij}}, \eta\right)$$
$$b_{ki}\gets O\left(b_{ki}, \dfrac{\partial l}{\partial b_{ki}}, \eta\right)$$
就可以得到较优的参数
反向传播
现在,我们来说说如何求出 $\dfrac{\partial l}{\partial w_{kij}}$ 和 $\dfrac{\partial l}{\partial b_{ki}}$ ,这也是最难的一部分
高能预警,请有一定的微分基础后再往下读
首先,根据 $q_{ki}=\sum_{j=1}^{n_{k-1}}w_{kij}r_{{k-1}j}+b_{ki}$ ,我们得出
$$
\begin{align*}
\dfrac{\partial l}{\partial w_{kij}}&=\dfrac{\partial l}{\partial q_{ki}}\cdot\dfrac{\partial q_{ki}}{\partial w_{kij}}\\
&=\dfrac{\partial l}{\partial q_{ki}}\cdot r_{{k-1}j}
\end{align*}
$$
$$
\begin{align*}
\dfrac{\partial l}{\partial b_{ki}}&=\dfrac{\partial l}{\partial q_{ki}}\cdot\dfrac{\partial q_{ki}}{\partial b_{ki}}\\
&=\dfrac{\partial l}{\partial q_{ki}}
\end{align*}
$$
$$
\begin{align*}
\dfrac{\partial l}{\partial q_{ki}}&=\sum_{j=1}^{n_{k+1}}\dfrac{\partial l}{\partial q_{{k+1}j}}\cdot\dfrac{\partial q_{{k+1}j}}{\partial r_{ki}}\cdot\dfrac{\partial r_{ki}}{\partial q_{ki}}\\
&=\sum_{j=1}^{n_{k+1}}\dfrac{\partial l}{\partial q_{{k+1}j}}\cdot w_{{k+1}ji}\cdot f_k^{’}(q_{ki})\\
&=\left(\sum_{j=1}^{n_{k+1}}\dfrac{\partial l}{\partial q_{{k+1}j}}\cdot w_{{k+1}ji}\right)\cdot f_k^{’}(q_{ki})
\end{align*}
$$
根据 $l=L(r_{T1}, r_{T2}, … r_{Tn_T}, y_1, y_2, … y_{n_T})$ ,可以得出
$$
\begin{align*}
\dfrac{\partial l}{\partial q_{Ti}}&=\dfrac{\partial l}{\partial r_{Ti}}\cdot\dfrac{\partial r_{Ti}}{\partial q_{Ti}}\\
&=\dfrac{\partial l}{\partial r_{Ti}}\cdot f_T^{’}(q_{Ti})
\end{align*}
$$
得出了这几条公式,我们就能从后往前算出所有的 $\dfrac{\partial l}{\partial q_{ki}}$ ,再用它们求出所有的 $\dfrac{\partial l}{\partial w_{kij}}$ 和 $\dfrac{\partial l}{\partial b_{ki}}$ ,用来进行梯度下降
总结
总结起来,重要的公式无外乎这几个:
$$q_{ki}=\sum_{j=1}^{n_{k-1}}w_{kij}r_{{k-1}j}+b_{ki}$$
$$r_{ki}=f_k(q_{ki})$$
$$l=L(r_{T1}, r_{T2}, … r_{Tn_T}, y_1, y_2, … y_{n_T})$$
$$\dfrac{\partial l}{\partial q_{Ti}}=\dfrac{\partial l}{\partial r_{Ti}}\cdot f_T^{’}(q_{Ti})$$
$$\dfrac{\partial l}{\partial q_{ki}}=\left(\sum_{j=1}^{n_{k+1}}\dfrac{\partial l}{\partial q_{{k+1}j}}\cdot w_{{k+1}ji}\right)\cdot f_k^{’}(q_{ki})$$
$$\dfrac{\partial l}{\partial w_{kij}}=\dfrac{\partial l}{\partial q_{ki}}\cdot r_{{k-1}j}$$
$$\dfrac{\partial l}{\partial b_{ki}}=\dfrac{\partial l}{\partial q_{ki}}$$
$$w_{kij}\gets O\left(w_{kij}, \dfrac{\partial l}{\partial w_{kij}}, \eta\right)$$
$$b_{ki}\gets O\left(b_{ki}, \dfrac{\partial l}{\partial b_{ki}}, \eta\right)$$
再谈训练
在训练一个模型时,需要将数据集分成两部分:训练集和测试集
测试集不能以任何形式参与训练,仅用于测试模型准确性
若模型在训练集上表现优异,但在测试集上表现不佳,可能是出现了过拟合,这时可以通过减少网络层数和增加训练集的数据量来解决
另一种解决方法是使用正则化
以L2正则化为例,它会使用
$$J(\lambda, w_{111}, w_{112}, … w_{Tn_Tn_{T-1}}, b_{11}, b_{12}, … b_{Tn_T}, x_1, x_2, … x_{n_T}, y_1, y_2, … y_{n_T})=L(x_1, x_2, … x_{n_T}, y_1, y_2, … y_{n_T})+\lambda(\sum_{k=1}^{T}\sum_{i=1}^{n_k}\sum_{j=1}^{n_{k-1}}w_{kij}^2+\sum_{k=1}^{T}\sum_{i=1}^{n_k}b_{ki}^2)$$
替代原本的损失函数,其中 $L(x_1, x_2, … x_{n_T}, y_1, y_2, … y_{n_T})$ 是原本的损失函数, $w$ 和 $b$ 是网络的边权和偏置
同时求微分公式改为
$$\dfrac{\partial l}{\partial w_{kij}}=\dfrac{\partial l}{\partial q_{ki}}\cdot r_{{k-1}j}+2\lambda w_{kij}$$
$$\dfrac{\partial l}{\partial b_{ki}}=\dfrac{\partial l}{\partial q_{ki}}+2\lambda b_{ki}$$
$\lambda$ 是正则化因子,是超参数
$\lambda$ 值越大,网络中的参数会偏向于更小以降低损失值,同时防止过拟合
还有一种常用的正则化方法 Dropout ,它通过在训练时随机忽略一部分神经元来防止过拟合,读者可以自行了解
演示代码
这份代码实现了一个分类器,并用异或问题进行测试
它不支持正则化和不同的激活函数
年代久远,风格不一致请见谅
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
| #include<vector>
#include<random>
#include<functional>
class FeedforwardNeuralNetwork
{
public:
FeedforwardNeuralNetwork(std::mt19937 *const &randomNumberGeneration,const unsigned &inNum,const std::vector<unsigned> &neuralNum,const std::function<double(const double&)> &activationFunction,const std::function<double(const double&)> &activationFunctionDerivative);
std::vector<double> calculate(const std::vector<double> &in) const;
void train(const std::vector<double> &in,const std::vector<double> &desiredOut,const double &learningRate);
private:
class NeuralLayer
{
public:
NeuralLayer(std::mt19937 *const &randomNumberGeneration,const unsigned &neuralNumForLastLayer,const unsigned &neuralNumForThisLayer,const std::function<double(const double&)> &activationFunction,const std::function<double(const double&)> &activationFunctionDerivative);
std::pair<std::vector<double>,std::vector<double> > forward(const std::vector<double> &outForLastLayer) const;
std::vector<double> backward(const std::vector<double> &inForThisLayer,const std::vector<double> &outForThisLayer,const std::vector<double> &desiredOut) const;
std::vector<double> backward(const std::vector<double> &inForThisLayer,const std::vector<std::vector<double> > &weightForNextLayer,const std::vector<double> &gradientForNextLayer) const;
void adjust(const std::vector<double> &outForLastLayer,const std::vector<double> &gradientForThisLayer,const double &learningRate);
std::vector<std::vector<double> > weight;
std::vector<double> bias;
const std::function<double(const double&)> activationFunction;
const std::function<double(const double&)> activationFunctionDerivative;
};
std::vector<std::pair<std::vector<double>,std::vector<double> > > forward(const std::vector<double> &in) const;
std::vector<std::vector<double> > backward(const std::vector<std::pair<std::vector<double>,std::vector<double> > > &ans,const std::vector<double> &desiredOut) const;
void adjust(const std::vector<double> &in,const std::vector<std::vector<double> > &outForEachLayer,const std::vector<std::vector<double> > &gradientForEachLayer,const double &learningRate);
public:
std::vector<NeuralLayer> layer;
};
FeedforwardNeuralNetwork::FeedforwardNeuralNetwork(std::mt19937 *const &randomNumberGeneration,const unsigned &inNum,const std::vector<unsigned> &neuralNum,const std::function<double(const double&)> &activationFunction,const std::function<double(const double&)> &activationFunctionDerivative)
{
for(unsigned i=1;i<=neuralNum.size();i++)
layer.push_back(i<2?NeuralLayer(randomNumberGeneration,inNum,neuralNum.at(i-1),activationFunction,activationFunctionDerivative):NeuralLayer(randomNumberGeneration,neuralNum.at(i-2),neuralNum.at(i-1),activationFunction,activationFunctionDerivative));
}
std::vector<double> FeedforwardNeuralNetwork::calculate(const std::vector<double> &in) const //输出最终结果
{
return forward(in).back().second;
}
void FeedforwardNeuralNetwork::train(const std::vector<double> &in,const std::vector<double> &desiredOut,const double &learningRate)
{
std::vector<std::pair<std::vector<double>,std::vector<double> > > ans=forward(in);
std::vector<std::vector<double> > gradient=backward(ans,desiredOut);
std::vector<std::vector<double> > outForEachLayer;
for(unsigned i=1;i<=layer.size();i++)
outForEachLayer.push_back(ans.at(i-1).second);
adjust(in,outForEachLayer,gradient,learningRate);
}
FeedforwardNeuralNetwork::NeuralLayer::NeuralLayer(std::mt19937 *const &randomNumberGeneration,const unsigned &neuralNumForLastLayer,const unsigned &neuralNumForThisLayer,const std::function<double(const double&)> &_activationFunction,const std::function<double(const double&)> &_activationFunctionDerivative):
activationFunction(_activationFunction),
activationFunctionDerivative(_activationFunctionDerivative)
{
for(unsigned i=1;i<=neuralNumForThisLayer;i++)
{
weight.push_back(std::vector<double>());
for(unsigned j=1;j<=neuralNumForLastLayer;j++)
weight[i-1].push_back((*randomNumberGeneration)()/(double)0xffffffff*2.0-1.0);
bias.push_back((*randomNumberGeneration)()/(double)0xffffffff*2.0-1.0);
}
}
std::pair<std::vector<double>,std::vector<double> > FeedforwardNeuralNetwork::NeuralLayer::forward(const std::vector<double> &outForLastLayer) const //前向传播
{
std::vector<double> in; //激活前
std::vector<double> out;//激活后
for(unsigned i=1;i<=weight.size();i++)
{
in.push_back(0.0);
for(unsigned j=1;j<=weight.at(i-1).size();j++)
in[i-1]+=outForLastLayer.at(j-1)*weight.at(i-1).at(j-1);
in[i-1]+=bias.at(i-1);
out.push_back(activationFunction(in[i-1]));
}
return make_pair(in,out);
}
std::vector<double> FeedforwardNeuralNetwork::NeuralLayer::backward(const std::vector<double> &inForThisLayer,const std::vector<double> &outForThisLayer,const std::vector<double> &desiredOut) const //计算输出层局部微分
{
std::vector<double> gradient;
for(unsigned i=1;i<=weight.size();i++)
gradient.push_back(2*(outForThisLayer.at(i-1)-desiredOut.at(i-1))*activationFunctionDerivative(inForThisLayer.at(i-1)));
return gradient;
}
std::vector<double> FeedforwardNeuralNetwork::NeuralLayer::backward(const std::vector<double> &inForThisLayer,const std::vector<std::vector<double> > &weightForNextLayer,const std::vector<double> &gradientForNextLayer) const //计算隐藏层局部微分
{
std::vector<double> gradient;
for(unsigned i=1;i<=weight.size();i++)
gradient.push_back(0.0);
for(unsigned i=1;i<=weightForNextLayer.size();i++)
for(unsigned j=1;j<=weightForNextLayer.at(i-1).size();j++)
gradient[j-1]+=weightForNextLayer.at(i-1).at(j-1)*gradientForNextLayer.at(i-1);
for(unsigned i=1;i<=gradient.size();i++)
gradient[i-1]*=activationFunctionDerivative(inForThisLayer.at(i-1));
return gradient;
}
void FeedforwardNeuralNetwork::NeuralLayer::adjust(const std::vector<double> &outForLastLayer,const std::vector<double> &gradientForThisLayer,const double &learningRate) //调整参数
{
for(unsigned i=1;i<=weight.size();i++)
for(unsigned j=1;j<=weight.at(i-1).size();j++)
weight[i-1][j-1]-=learningRate*gradientForThisLayer.at(i-1)*outForLastLayer.at(j-1);
for(unsigned i=1;i<=bias.size();i++)
bias[i-1]-=learningRate*gradientForThisLayer.at(i-1);
}
std::vector<std::pair<std::vector<double>,std::vector<double> > > FeedforwardNeuralNetwork::forward(const std::vector<double> &in) const
{
std::vector<std::pair<std::vector<double>,std::vector<double> > > ans;
for(unsigned i=1;i<=layer.size();i++)
ans.push_back(layer.at(i-1).forward(i<2?in:ans.at(i-2).second));
return ans;
}
std::vector<std::vector<double> > FeedforwardNeuralNetwork::backward(const std::vector<std::pair<std::vector<double>,std::vector<double> > > &ans,const std::vector<double> &desiredOut) const
{
std::vector<std::vector<double> > gradient;
for(unsigned i=layer.size();i>=1;i--)
if(i==layer.size())
gradient.push_back(layer.at(i-1).backward(ans.at(i-1).first,ans.at(i-1).second,desiredOut));
else
gradient.push_back(layer.at(i-1).backward(ans.at(i-1).first,layer.at(i).weight,gradient.at(layer.size()-i-1)));
for(unsigned i=1,j=gradient.size();i<j;i++,j--)
swap(gradient[i-1],gradient[j-1]);
return gradient;
}
void FeedforwardNeuralNetwork::adjust(const std::vector<double> &in,const std::vector<std::vector<double> > &outForEachLayer,const std::vector<std::vector<double> > &gradientForEachLayer,const double &learningRate)
{
for(unsigned i=1;i<=layer.size();i++)
layer[i-1].adjust(i<2?in:outForEachLayer.at(i-2),gradientForEachLayer.at(i-1),learningRate);
}
#include<math.h>
#define E 2.7182818284590452353602874713526624977572470936999595749669676277240766303535475945713821785251664274
double Sigmoid(const double &a)
{
return 1.0/(1.0+pow(E,-a));
}
double SigmoidDerivative(const double &a)
{
return Sigmoid(a)*(1-Sigmoid(a));
}
#undef E
#include<math.h>
#define E 2.7182818284590452353602874713526624977572470936999595749669676277240766303535475945713821785251664274
double Tanh(const double &a)
{
return (pow(E,a)-pow(E,-a))/(pow(E,a)+pow(E,-a));
}
double TanhDerivative(const double &a)
{
return (4.0*pow(E,2.0*a))/((pow(E,2.0*a)+1.0)*(pow(E,2.0*a)+1.0));
}
#undef E
double ReLU(const double &a)
{
if(a>0.0)
return a;
else
return 0.0;
}
double ReLUDerivative(const double &a)
{
if(a>=0.0)
return 1.0;
else
return 0.0;
}
#include<stdio.h>
void printNetwork(const FeedforwardNeuralNetwork &network)
{
for(unsigned i=1;i<=network.layer.size();i++)
{
printf("Layer %u:\n",i);
for(unsigned j=1;j<=network.layer.at(i-1).weight.size();j++)
{
printf(" Node %u:\n",j);
printf(" Weight:");
for(unsigned k=1;k<=network.layer.at(i-1).weight.at(j-1).size();k++)
printf("%lf ",network.layer.at(i-1).weight.at(j-1).at(k-1));
printf("\n");
printf(" Bias:%lf\n",network.layer.at(i-1).bias.at(j-1));
}
}
printf("\n");
}
void train(FeedforwardNeuralNetwork *const &network,const std::vector<std::pair<std::vector<double>,std::vector<double> > > &trainSet,const double &learningRate,const unsigned &roundNum,const unsigned &frequency=1)
{
printf("Start train\n");
for(unsigned k=1;k<=roundNum;k++)
{
double loss=0.0;
for(unsigned i=1;i<=trainSet.size();i++)
{
network->train(trainSet.at(i-1).first,trainSet.at(i-1).second,learningRate);
std::vector<double> out(network->calculate(trainSet.at(i-1).first));
for(unsigned j=1;j<=out.size();j++)
loss+=(trainSet.at(i-1).second.at(j-1)-out.at(j-1))*(trainSet.at(i-1).second.at(j-1)-out.at(j-1));
if(k%frequency==0)
{
printf("In:[");
for(unsigned j=1;j<=trainSet.at(i-1).first.size();j++)
printf("%lf,",trainSet.at(i-1).first.at(j-1));
printf("]\nDesired Out:[");
for(unsigned j=1;j<=trainSet.at(i-1).second.size();j++)
printf("%lf,",trainSet.at(i-1).second.at(j-1));
printf("]\nOut:[");
for(unsigned j=1;j<=out.size();j++)
printf("%lf,",out.at(j-1));
printf("]\n\n");
}
}
loss/=trainSet.size();
if(k%frequency==0)
{
printf("Loss:%lf\n",loss);
printNetwork(*network);
}
}
printf("Finished train\n");
}
void test(FeedforwardNeuralNetwork *const &network,const std::vector<std::pair<std::vector<double>,std::vector<double> > > &testSet)
{
printf("Start test\n");
double loss=0.0;
for(unsigned i=1;i<=testSet.size();i++)
{
std::vector<double> out(network->calculate(testSet.at(i-1).first));
for(unsigned j=1;j<=out.size();j++)
loss+=(testSet.at(i-1).second.at(j-1)-out.at(j-1))*(testSet.at(i-1).second.at(j-1)-out.at(j-1));
printf("In:[");
for(unsigned j=1;j<=testSet.at(i-1).first.size();j++)
printf("%lf,",testSet.at(i-1).first.at(j-1));
printf("]\nDesired Out:[");
for(unsigned j=1;j<=testSet.at(i-1).second.size();j++)
printf("%lf,",testSet.at(i-1).second.at(j-1));
printf("]\nOut:[");
for(unsigned j=1;j<=out.size();j++)
printf("%lf,",out.at(j-1));
printf("]\n\n");
}
loss/=testSet.size();
printf("Loss:%lf\n",loss);
printf("Finished test\n");
}
#include <ctime>
#include <random>
int main() {
std::mt19937 randomNumberGeneration(time(nullptr));
unsigned inNum = 2;
std::vector<unsigned> neuralNum;
neuralNum.push_back(3);
neuralNum.push_back(3);
neuralNum.push_back(1);
FeedforwardNeuralNetwork network(&randomNumberGeneration, inNum, neuralNum, std::bind(Sigmoid, std::placeholders::_1), std::bind(SigmoidDerivative, std::placeholders::_1));
std::vector<std::pair<std::vector<double>,std::vector<double> > > trainSet;
for(int i = 1; i <= 10000; i++) {
std::vector<double> in;
in.push_back(randomNumberGeneration()/(double)0xffffffff*20.0-10.0);
in.push_back(randomNumberGeneration()/(double)0xffffffff*20.0-10.0);
std::vector<double> out;
if(in.at(0) > 0.0) {
if(in.at(1) > 0.0) {
out.push_back(1.0);
} else {
out.push_back(0.0);
}
} else {
if(in.at(1) > 0.0) {
out.push_back(0.0);
} else {
out.push_back(1.0);
}
}
trainSet.push_back(std::make_pair(in, out));
}
std::vector<std::pair<std::vector<double>,std::vector<double> > > testSet;
for(int i = 1; i <= 50; i++) {
std::vector<double> in;
in.push_back(randomNumberGeneration()/(double)0xffffffff*20.0-10.0);
in.push_back(randomNumberGeneration()/(double)0xffffffff*20.0-10.0);
std::vector<double> out;
if(in.at(0) > 0.0) {
if(in.at(1) > 0.0) {
out.push_back(1.0);
} else {
out.push_back(0.0);
}
} else {
if(in.at(1) > 0.0) {
out.push_back(0.0);
} else {
out.push_back(1.0);
}
}
testSet.push_back(std::make_pair(in, out));
}
train(&network, trainSet, 0.03, 100, 10);
test(&network, testSet);
}
|

